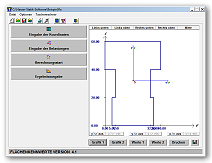
Beschreibung des Moduls
Flächenkennwerte

Mit dem Programm Flächenkennwerte sind Sie in der Lage, für sämtliche polygonal begrenzten Flächen alle technisch wichtigen Kennwerte wie Fläche, Trägheitsmomente, Hauptachsen, Trägheitshalbmesser und Widerstandsmomente zu berechnen.
Möglichkeiten
Weitere Möglichkeiten:
Weiterhin ist es möglich, nach Eingabe von Belastungen wie Längskraft oder Momente, die Spannungen in allen Eckpunkten des Querschnittes berechnen und grafisch darstellen zu lassen.
Als Grundlage für die Berechnung dienen die Formeln nach Fleßner, welche aus den Flächenintegralen nach Gauß abgeleitet wurden.

Eingabe
Die Eingabe:
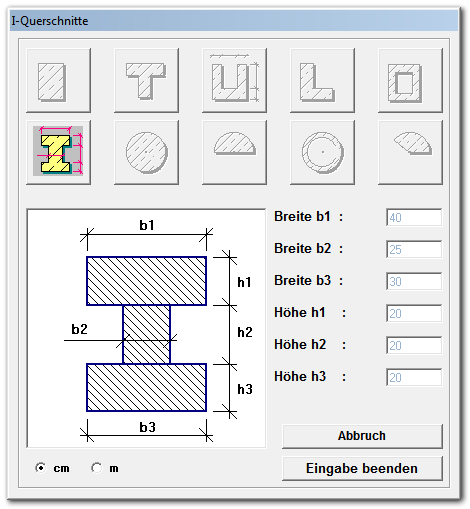
Die Eingabe des Querschnittes erfolgt über Koordinaten. Alternativ können typische Querschnitte über einen Generator definiert werden. Folgende häufig vorkommenden Querschnitte können definiert werden:

Bei Wahl eines "Typischen Querschnittes" werden die Maße tabellarisch eingegebn und die Koordinaten automatisch ermittelt:

Ergebnisse
Die Ergebnisausgabe:

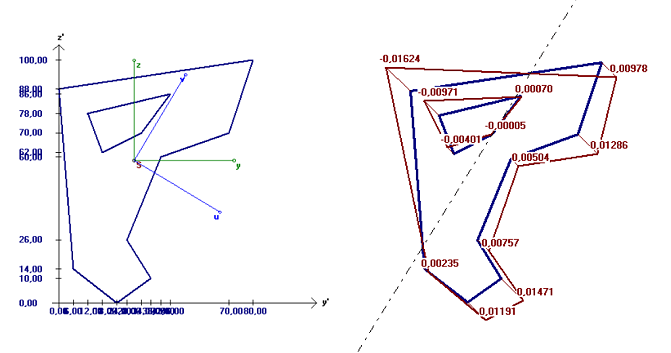
Zunächst kann der definierte Querschnitt grafisch dargestellt werden: Grafik 1.

Wenn Belastungen eingegeben wurden, können die Spannungen ebenfalls angezeigt werden: Grafik 2.

Folgende Ergebniswerte werden ausgegeben:


Berechnungsgrundlagen
Berechnungsgrundlagen:
Zur Berechnung von Flächen, welche eine polygonartige Umrandung aufweisen, wurden die nachfolgenden Formeln entwickelt, welche sich besonders für die Computerprogrammierung eignen.
Zuerst wählt man zur Eingabe der Eckpunktkoordinaten ein übergeordnetes Koordinatensystem y` / z`. Bezogen auf dieses Koordinatensystem werden dann die Fläche (A), alle statischen Momente ersten Grades (Sy`/ Sz`) und alle statischen Momente zweiten Grades (Iy`/ Iz`/ Iyz`) berechnet.
Im nächsten Schritt wird aus den ermittelten Werten die Lage des Schwerpunktes der betrachteten Fläche errechnet. Die Verschiebung des Koordinatensystems in den Schwerpunkt erfolgt durch die Berechnung der Kennwerte nach dem Satz von Steiner, wonach die Flächen mal dem jeweiligen, quadrierten Abstand, von den zuvor errechneten und auf das übergeordnete Koordinatensystem bezogenen statischen Momenten zweiten Grades abgezogen werden.
Mit Hilfe dieser Kenngrößen kann man nun die Hauptachsen und die zugehörigen Werte wie Imax / Imin (Iu /Iv) , die Trägheitshalbmesser iu und iv sowie den Winkel Alpha, um den das Hauptachssystem verdreht ist.
Anschließend werden die Koordinaten der Eckpunkte in das Hauptachskoordinatensystem transformiert. Teilt man dann die Hauptträgheitsmomente durch die Abstände der vom Schwerpunkt entferntest liegenden Punkte, so erhält man die Widerstandsmomente (Momente dritten Grades maxWu, minWu, maxWv, minWv).
Nachdem alle Kennwerte des Querschnittes ermittelt wurden, kann man nun die Spannungen Sigma (in kN/cm²) in den Eckpunkten des Querschnittes ausrechnen.

Der Berechnung im Programm liegen folgende Formeln zugrunde :
Für die Spannungen
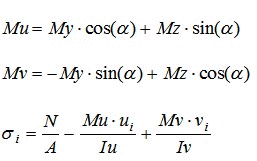
Gleichung der Nullinie
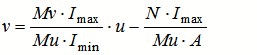
Für die Flächenkennwerte
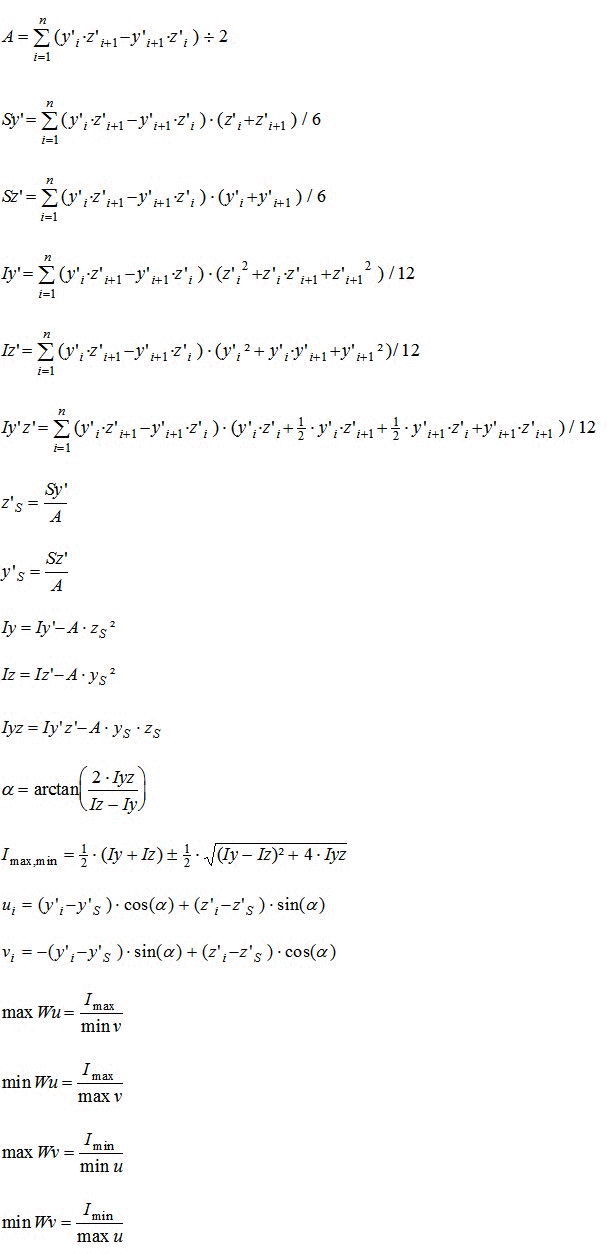


Weitere Screenshots: Bild klicken.


 |
Beispiel 1: Beliebiger Querschnitt mit Öffnung |
 |
Beispiel 2: Standardquerschnitt Doppel-T |


Das Programm Flächenkennwerte wird regelmäßig weiterentwickelt. Folgende Tabelle zeigt den aktuellen Entwicklungsstand:
15/12.1
• Wy,min/max und Wz,min/max werden nun auch noch mit ausgegeben
12/04.1
![]() Umstellung / Ergänzung auf Eurocode
Umstellung / Ergänzung auf Eurocode
11/06.1
• Korrektur bei geteilten Querschnitten

Änderungen / Erweiterungen vor 2010 werden hier nicht aufgelistet. Für Informationen über Versionen 09/11.1 und älter klicken Sie bitte hier.